World Coordinates and Image coordinates
Pinhole Camera Model
$$ x = K \left[ \begin{array}{ll} R & t \end{array} \right] x $$x: Image Coordinates: $(u, v, 1)$ K: Intrinsic Matrix $(3 \times 3)$ R: Rotation $(3 \times 3)$ t: Translation $(3 \times 1)$ X: World Coordinates: $(X, Y, Z, 1)$
Basically, from the right side to the leftside, it is transforming a point (1) from the world coordinates to camera coordinates, and then project the point (2) from camera coordinates down to the image plane.
(1) is done by the $\left[\begin{array}{ll} R & t \end{array}\right]$, the extrinsic matrix (rotation and translation).
(2) is done by K, the intrinsic/projection matrix.
The Intrinsic Matrix
How we do the projection?
First, let’s look at this projection from camera coordinate to image plane.
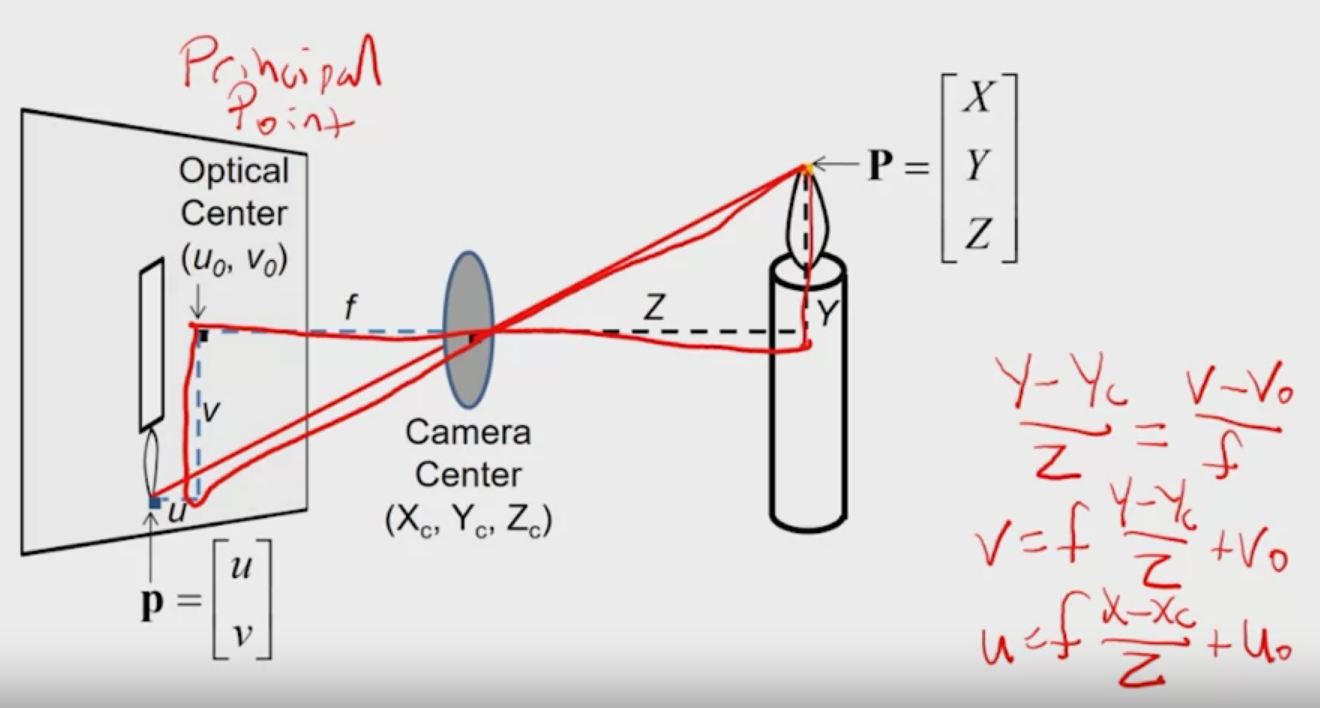
In a matrix form, if we set the camera center at $(0, 0, 0)$, this is actually easy to express:
Now if we just use the default R and t, the model is:
The Extrinsic Matrix
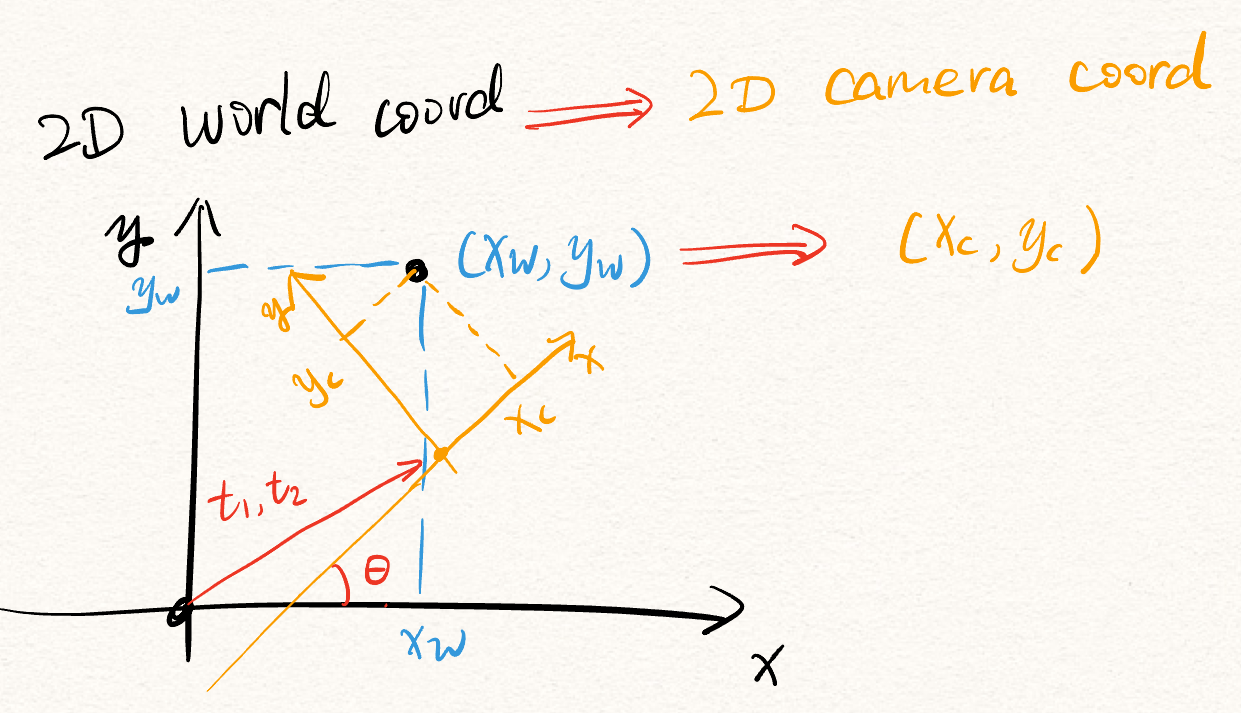
The R here is the rotation matrix for 3D coordinate. World coordinate $\xrightarrow{\text{rotate to }}$ Camera coordinate direction. This R is also orthonormal.
The t here traslates the world origin to the camera center.
If we know that position $(x, y, z)$ of the camera in the world coordinate, we can also set up this simple equation for calculating R and t.
The Complete Model
Exercise Take home question 1:
Suppose the camera axis is in the direction of $(x=0, y=0, z=1)$ in its own coordinate system. What is the camera axis in world coordinates given the extrinsic parameters $R, t$ ?
Solution
Note that this is not asking the projection on 2D image, but it is asking: after the rotation what is the direction of this camera?
Let $X_c$ denote the direction of this camera in its own coordinate. So $X_c=\left[\begin{array}{l}0 \\ 0 \\ 1\end{array}\right]$ Let $X_w$ denote the direction of this camera in world coordinate. So $\quad X_w=\left[\begin{array}{l}x_w \\ y_w \\ z_w\end{array}\right]$ We have equation:
\begin{align*} X_c & =\left[ \begin{array}{ll} R & t \end{array} \right] \left[ \begin{array}{c} X_w \\ 1 \end{array} \right] \\ X_c & =R X_w+t \\ R X_w & =X_c-t \\ X_w & =R^{-1}\left(X_c-t\right) \\ & =R^{-1} X_c-R^{-1} t\\ & =R^{T} X_c-R^{T} t \quad \text { as } R^{-1}=R^{T} \\ \end{align*}
When we consider just the direction, translation doesn’t matter. So:
$$ X_w=R^T X_c $$Exercise Take home question 2:
Suppose a camera at height $y=h,(x=0, z=0)$ observes a point at $(u, v)$ known to be on the ground $(y=0)$. Assume $R$ is identity. What is the 3D position of the point in terms of $f, u_0, v_0$ ?
Solution:
The camera is at $(x, y, z) = (0, h, 0)$. And since we know that the rotation matrix R is an identity matrix, we can set up an equation to solve for t:
\begin{align*} X_{cc} & =\left[\begin{array}{ll} I & t \end{array}\right]\left[\begin{array}{c} X_{cw} \\ 1 \end{array}\right]=X_{cw}+t=0 \\ \Rightarrow t & =-X_{cw} = \left[ \begin{array}{c} 0\\ -h\\ 0\\ \end{array} \right] \end{align*}
Where $X_{cc}$ stands for the position of camera at camera coordinate. $X_{cw}$ stands for the position of camera at world coordinate.
Then, we know that in the camera coordinate, the point is observed at $(u, v)$. This fills in the left side of the Pinhole Camera Model.
We want to solve for the position $X_{pw}$ of the point in the world coordinate. We also know that this point is on the ground, so its $y$ value is 0. As we have all the information we want, writing out the formula of the Pinhole Camera Model and we should be able to solve the problem:
Reference
CS445 Derek Hoiem: https://courses.engr.illinois.edu/cs445/fa2023/