Texture Synthesis & Hole Filling

Texture

Texture depicts spacially repeating patterns.

Texture Synthesis

Create new samples of a given texture. Many applications: virtual environments, hole-filling, texturing surfaces.

The challenge:

Need to model the whole spectrum: from repeated to stochastic texture.

One idea:

  1. Compute statistics of input texture
  2. Generate a new texture that keeps those same statistics.

But it is hard to model those probabilities distributions.

Another idea: ==Efros & Leung algorithm==

How to match patches?

  • Gaussian-weighted SSD (sum square difference) gives us more emphasis on nearby pixels.

$$ \text{SSD}(P, Q) = \sum_{i, j}(p_{ij} - q_{ij})^2 w_{ij}\ \text{where } w_{ij} = e^{ \frac{-(1-w/2)^2 - (j - h/2)^2}{2 \sigma^2} } $$

where $P$, and $Q$, are two patches, $w$ and $h$ in the $w_{ij}$ is the width and height of the patch.

  • What order to fill in new pixels?

    • “Onion skin” order: pixels with most neighbors are synthesized first.

How big should the patches be? The size of neighborhood window decides how stochasticity of the texture. A smaller window size gives a more random output.

$\boldsymbol{\textsf{Texture synthesis algorithm}}$

While image not filled:

  1. Get unfilled pixels with filled neighbors, sorted by the numebr of filled neighbors. (priority queue?)
  2. For each pixel, get top N matches based on visible neighbors. This is where we use the Gaussian-weighted SSD.
  3. Randomly select one of the matches and copy pixels from it.

This algorithm can be used for hole filling, extrapolation, …

Hole Filling

Sometimes, we can add more weights for the continuos edges when peforming the onion filling. (Gradient sensitive)

The Efros & Leung texture synthesis algorithm is simple and good, but too slow…

The next iteration is: Image quilting (Efros & Freeman 2001).

It depends on the observation that: neighbor pixels are highly correlated. Now, instead of filling pixel by pixel, we fill block by block.

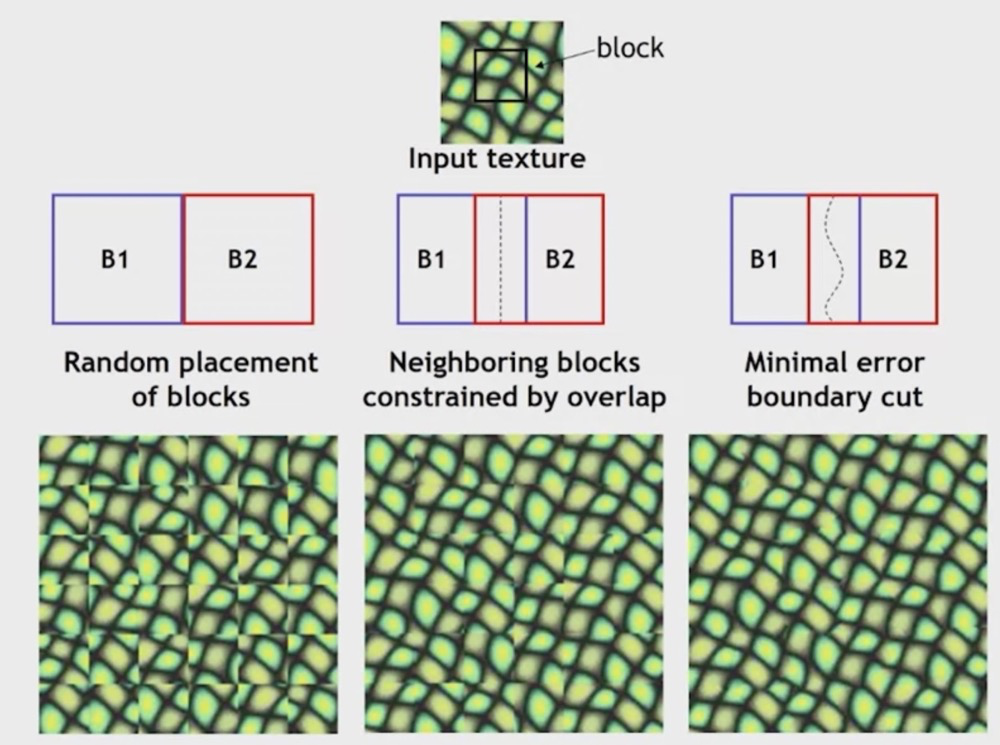
image-20230915005500901 image-20230915011020137

We need to put the tiles together. To make them look seemless, we can use this minimal error boundary cut. We calculate the square difference of the overlapping part, and calcualte the boundary. Using this simplified Dijikstra’s algorithm, we can easy calculate what we want.