The goal is to compare three methods for supporting keyword feature in PIR: Key-value filter in ChalametPIR, Sparse PIR, and the Cuckoo hashing method. In the beginning, we don’t want to start by comparing the detailed experimental performances, but we want to list their properties. What they are good / bad at.
Metrics
- Client storage
- Client computation
- Online communication
- Download size
- Offline communication (if any)
- Server storage
- Server computation
- Ability to support multiple clients
Notations:
$m$: the number of key-value pairs.
$k$: normally this stands for a key in one key-value pair.
DB: database in the server.
$N$: the number of entries in the database. This is not $m$.
Choice of filters
Paper: Binary Fuse Filters: Fast and Smaller Than Xor Filters.
Cuckoo hashing
Storage space
- range from 30 to 40% of the theoretial lower bound
Query(computation) time
- almost the same as 4-wise BF
Construction time
- Close to XOR filter almost times compared to BF
Failure probability
We have a detailed analysis in this paper, which basically suggesting that using 3 hash function, instead of 2, has smaller failure probability during construction.
Summary: let $N = çm$ be the size of the hash table. When $ç \geq 8$ and when we use 2 hash functions, the hashing failure is $2^{-\lambda}$, where
$$ \lambda=(1+0.65 s)\left(3.3 \log _2(ç)+\log _2(N)-0.8\right) $$The catch for 2 hash functions case: if we set $ç = 2$, $\lambda$ converges to 1 quickly. So, half of the time the construction of the database fails. But we can try a few more times. The failure rate is geometrically decreasing.
In 3 hash functions case, if $ç = 3$, we find $\lambda \approx 100$.
Binary fuse filter
- Storage space
- 3-wise BF: 13% of the theoretial lower bound
- 4-wise BF: 8% of the theoretial lower bound
- Query(computation) time
- 3-wise BF: Slightly better than 4-wise BF, almost the same as XOR filter
- 4-wise BF: Slightly worse than 3-wise BF, almost the same as Cuckoo hashing
- Construction time
- 3-wise BF: Slightly worse than 4-wise BF
- 4-wise BF: Slightly better than 3-wise BF
Notes:
- BF filter are generally much superior than cuckoo hashing except the query time is very close to 4-wise BF.
- 3-wise BF takes up more storage to trade for faster query response, compared to 4-wise BF.
TODO: Check out Ribbon filter. It is also better than Cuckoo hashing and XOR filter. In this paper it is claimed that binary fuse is better than Ribbon. Is it so? Is it suitable to our scheme (stateful and stateless)?
Let’s start by investigating how they realize the keyword PIR feature.
Cuckoo Hashing based on Onion
The paper Communication–Computation Trade-offs in PIR brought up a very simple method for realizing the keyword support.
Server initialize $\kappa$ cuckoo hash table defined by $\kappa$ hash functions $\mathrm{H}_1, \mathrm{H}_2$ and insert all the key-value pairs. This introduces $N = \kappa m$. $\kappa$ can be 2 or 3. We have analysis in the cuckoo hashing section.
After the database is configured, the client can use $\mathrm{H_1, \ldots, H_\kappa}$ to calculate the hash for the two positions. This is fast and easy. Then client initiates two PIR queries to get the two indices.
- Client storage
- $O(1)$ for hash functions + storage for PIR scheme. This is small
- Client computation.
- $O(1)$ for computing hashs + computation for PIR scheme.
- Online communication
- $\kappa$ PIR queries.
- Download size
- None.
- Offline communication (if any)
- None if in stateless PIR scheme.
- Server storage
- $N = 2m \approx $ twice as large as the PIR scheme it uses.
- Server computation
- Since $N = 2m$, this is also $\approx$ twice larger than a normal PIR scheme if we run the black box twice.
- Ability to support multiple clients
- Very easy. The server can share the two hash functions $\mathrm{H_1, H_2}$ to the public for client to download. The database is fixed.
Advantage:
This scheme works for all index-based PIR schemes. Both stateful and stateless. This completely uses PIR as a black box that stores the cuckoo hashing table as data.
Disadvantage:
2 or 3 $\times$ slower than the normal index-based PIR scheme if we assume computation time is proportional to the $N$.
SparsePIR based on Onion
We now focus on the original SparsePIR, not SparsePIR$^g$, not SparsePIR$^c$. So the scheme is based on a partition-based PIR. We have analysis in another file.
In here, $d_1 \in \set{128, 512, 1024}, \varepsilon = 0.38, b \approx 10000$.
- Client storage
- $O(1)$ 3 hash function key / seed + PIR scheme.
- Client computation
- $O(d_1) < 1024$ hash computation, which is very small. But requires preparing query vector for the PIR scheme of $b$ entries. Also not too bad.
- Online communication
- Query: $O(d_1)$ + a small PIR query.
- Response: equal to the size of one PIR response on database of size $m$. This is because they also need to touch on every entries.
- Download size
- None.
- Offline communication (if any)
- None.
- Server storage
- $(1+\varepsilon)m = (1 + 0.38)m = 1.38m$.
- $1.1m$ in SparsePIR$^{g}$.
- Server computation
- It requires minutes for preprocessing the database. $O(n)$.
- For the online runtime, SparsePIR requires many FHE dot product $\pmb{\mathrm{v_1}} \cdot \pmb{\mathrm{e}}_i, \forall i \in [b]$. I would like to learn about the experimental runtime for this part. ?????? DOT PRODUCT? There is no such thing here.
- Then, the server compute for a PIR query on $b$ many results we get from the previous step.
- Ability to support multiple clients
- This is also good enough.
Advantage:
The response size is the same as a normal index-based PIR scheme (Onion and Spiral here).
Disadvantage:
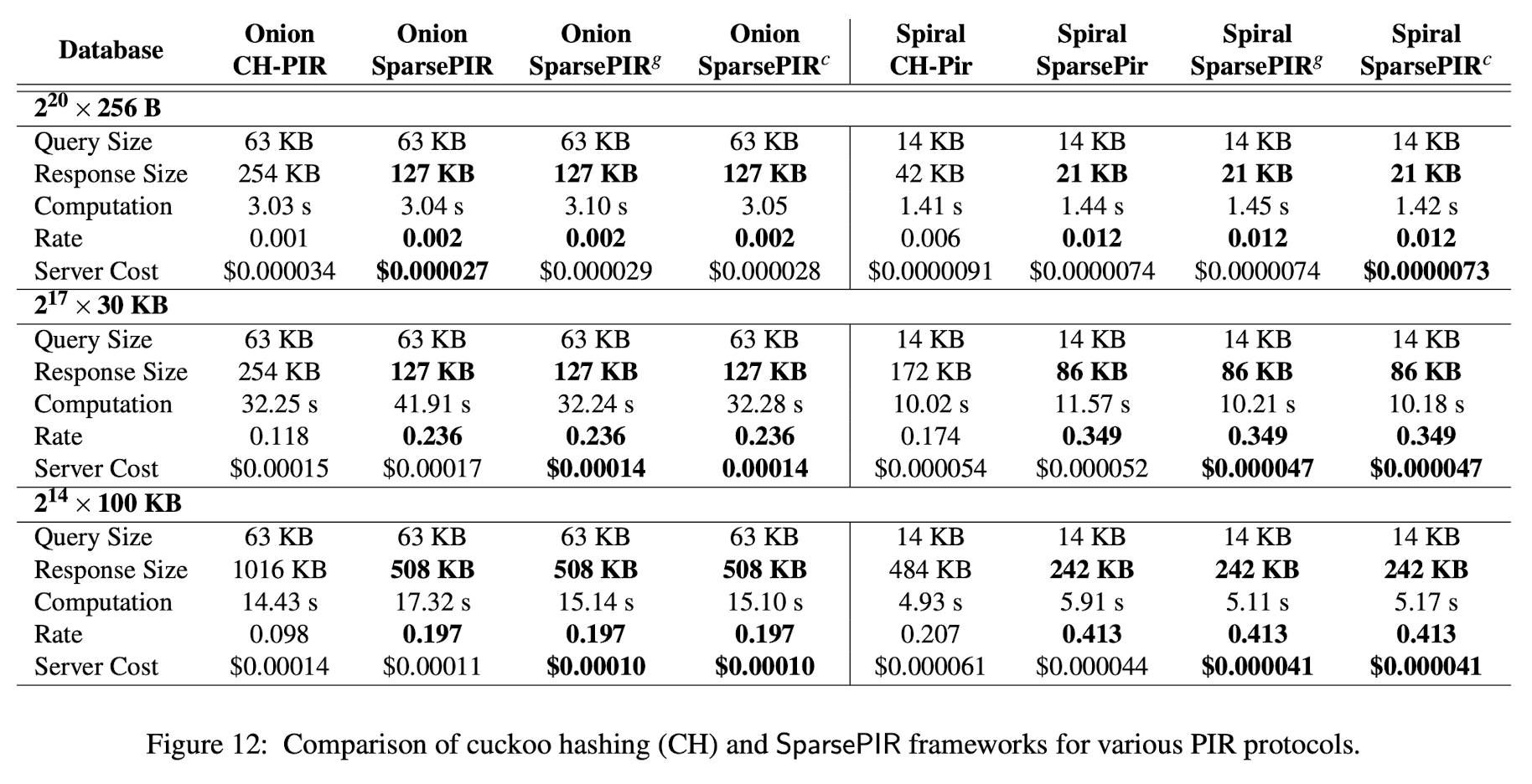
According to the data provided in their paper, we discover that they do not have any other advantages. The catch of this scheme is that computing the LWE dot product $\pmb{\mathrm{v_1}} \cdot \pmb{\mathrm{e}}_i, \forall i \in [b]$ is very slow. Say, when comparing the CH-PIR with SparsePIR, the cuckoo hashing method computes 2 PIR queries, but it is still faster than SparsePIR, which only computes a single PIR query on a 1281024$\times$ smaller “database” (do notice that the entry size is 1281024 larger, don’t know how to compare this as it involves LWE scheme). So, CH with a faster PIR scheme will likely outperform Sparse.
ChalametPIR Using Key-value Filter
The server uses 4 hash functions to store $m$ ke5y-value pairs in $N = ç m = 1.08m$ entries. 3 hash -> ç = 1.13. The hash functions are randomly generated by ther server. The server uses these 4 hash functions to generate the database. The performance depends on the Binary Fuse Filter (BFF). In the query state, the client uses the 4 hash functions to compute $\mathrm{H_1(k), H_2(k), H_3(k), H_4(k)}$ and does one of the the followings:
Client storage
- $O(1)$ for 3 or 4 hash funcitons (and client state if in stateful scheme).
Client computation
- negligible query ($O(n)$) and parsing ($O(1)$) time < 1 ms
Online communication
- One PIR query if use dot product in LWE scheme. This is
1 second in Frodo for 1 million 1KB elements. Note that the query size here is $O(N)$. The data in table 3 in ChalametPIR, the query size is about 12 ~ 18$\times$ larger than SpiralSparsePIR, about 14$\times$ larger than OnionSparsePIR. - If we don’t combine all indices in one query, then 4 queries on $N = 1.08m$ database or 3 queries on $N=1.13m$ database.
- One PIR query if use dot product in LWE scheme. This is
Download size
- Almost the same as Frodo PIR. Client must download the entire hint.
- $O(1)$ ~6MB
Offline communication (if any)
- The client downloads the hint from server.
Server storage
- Raw database has $N = ç m = 1.08m$ many enties when $k=4$.
- Nothing more if no server preprocessing.
Server computation
- This involves a LWE matrix vector multiplication.
- Slightly slower than the Frodo PIR scheme.
- O(m) 10e6 seconds for 218 × 1 kB DB
Ability to support multiple clients
- According to FrodoPIR, it is good at scaling.
Thoughts:
If we simply use PIR as a black box, the best we can do so far is to use key-value filter with 3 hash functions, and possibly add the results together on the server side to reduce response size. This assume that server computation is linear to the size of the database. Otherwise, cuckoo hashing should be better (less request size / fewer rounds). Example: in hint-based stateful PIR, both methods are solid. the difference is that in cuckoo hashing, server must return two partitions instead of one. If using key-value filter, consider false-positive rate and also the larger request size.
The way Sparse realize keyword support naturally combined with linear combination, which invovles in dot product. It is unlikely to be optimized anymore.
From this comparison, we want to quickly add cuckoo hashing method for the latest Onion-PIR.