The following is a note for my talk during Ling’s group meeting.

What is FHE?

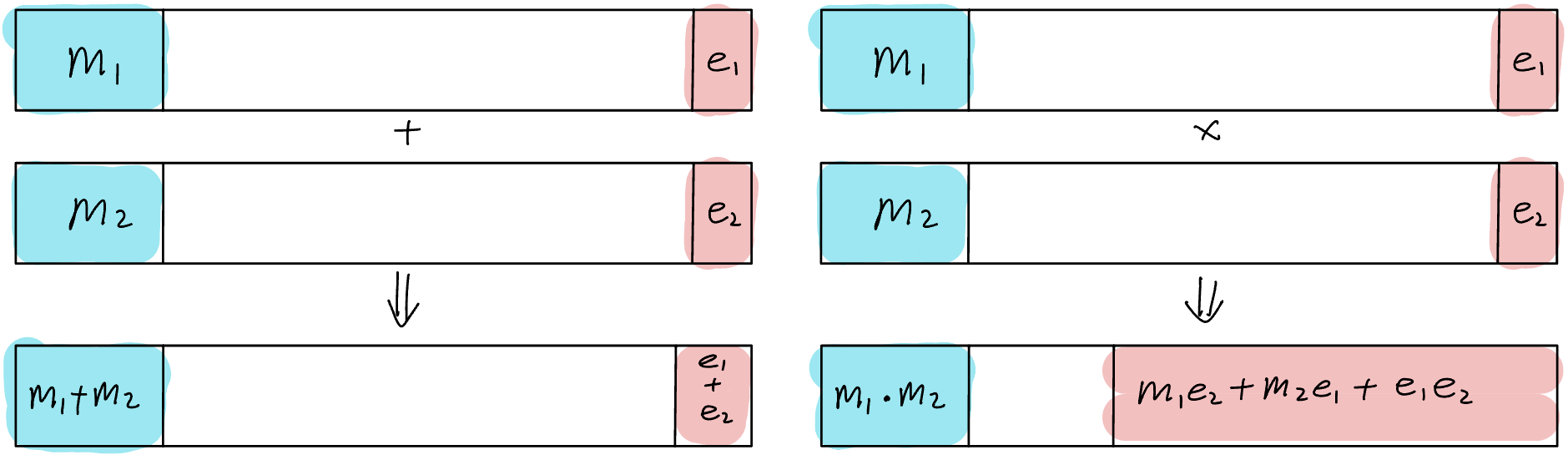
Homomorphic encryption allows some computation (addition, scalar multiplication, ct-ct multiplication) directly on ciphertexts without first having to decrypt it.

Partially Homomorphic Encryption support only one of those possible operation. RSA is an example: $$ \text{Enc}(m_1) \cdot \text{Enc}(m_2) = m_1^e \cdot m_2^e = (m_1 \cdot m_2)^e = \text{Enc}(m_1 \cdot m_2) $$

FHE supports Addition AND Scalar Multiplicaiton:

$$ \begin{cases} \text{Enc}(m_1) + \text{Enc}(m_2) = \text{Enc}(m_1 + m_2)\\ \text{Enc}(m) \cdot c = \text{Enc}(m \cdot c) \end{cases} $$
Fancy! And it exsists!

LWE & Ring-LWE

Hiding secrets by adding some noise.

Learning With Error (LWE)

Given a random vector $a \in \mathbb{Z}_q^n$, a secret key $s \in \mathbb{B}^n, \mathbb{B} = \set{0, 1}$, a small plaintext message $m \in \mathbb{Z}_t$ with $t \ll q$, and a small noise $e$ sampled from a gaussian distribution centered at 0: $$ \text{LWE}(m) = (a, a \cdot s + m + e) $$ $n$ decides the security level we want. The operator “$\cdot$” is a dot product.

The decryption is also straight forward in high-level: $$ \text{Dec}_s(;(a, b);) = \lfloor \varphi_s(;(a, b);)\rceil = \lfloor b - a \cdot s \rceil $$

Think of this: if we always encrypt $m = 0$. A “learning without error” scheme can be easily be solved by setting up $n$ linear equations. However, adding this error makes it very hard to solve. (Oded Regev?)

The definition I give here is not completely accurate. To encrypt $m$, one should sometimes scale it up or “shift to the left” so that the lower bits are reserved for noise.

Toy example: say $q = 2^{32}$, then we can use a 32 bit unsigned integer for each number. Suppose we allow $m$ to have 4 bits, and the rest $32 - 4 = 28$ lower bits are reserved for our noise.

Additions and scalar mulitiplications are intuitive. ct-ct multiplications needs special design. It’s possible!

BFV is a RLWE scheme that supports ct-ct multiplication. $(a_1, b_1) \cdot (a_2, b_2) = (a_1b_1, a_1b_2 + a_2b_1, b_1b_2)$.

#### Supporting larger message?

Notice that in the general definition for LWE, the message we can encrypt is $m \in \mathbb{Z}_t$. This is typically not enough. What if we want a larger message $\mu \in \mathbb{Z}_t^m$? Hence, we typically use a random matrix $A$ for encryption:

$$ \begin{align*} \text{LWE}(\mu) = (A, A \cdot s + \mu + e)\\ A \in \mathbb{Z}_q^{m \times n}, s \in \mathbb{B}^n, \mu \in \mathbb{Z}_t^m \end{align*} $$
This means that encrypting a vector in $\mathbb{Z}_t^m$ requires $mn$ many $\mathbb{Z}_q$. RLWE helps reduce this!

Ring Learning With Error (RLWE)

Ring variant of LWE. Instead of having $a$ as a vector, we upgrade all vector addition and scalar multiplication are upgraded to polynomial multiplications and additions. Now, we have $a \in \mathbb{Z}_q[x] / (x^n + 1), m \in \mathbb{Z}_t[x] / (x^n + 1), s \in \mathbb{B}[x] / (x^n + 1)$. $n$ is the polynomial degree. $q$ and $t$ are coefficient modulus for ciphertext and plaintext. Everything in polynoimal!

RLWE is more efficient:

  • " LWE problems tend to require rather large key sizes, typically on the order of $n^2$." (Regev’s survey) To use LWE, typically need $n$ linear equations with errors, each of them has size $n$ key. In RLWE, you only need $n$ coefficients.
  • Fast Fourier Transform and Number Theoretic Transform can be applied to polynomials. It makes computation faster!

The problem with noise growth

Addition has additive noise growth, multiplication has multiplicative noise growth. This is bad because we cannot perform this computation many times…

Good news: there is a way to make multiplications have additive noise growth.

Gadget Decomposition

How do you calculate $3405 \cdot 6$ by hand?

Simple gadget decomposition (special case):

For a message $m \in \mathbb{Z}$, we scale it to different powers: $$ \mathsf{Scale}(m) = m \cdot (10^{\ell - 1}, \ldots, 10^{0}) $$ This creates a vector of size $\ell$ for some chosen number $\ell$. Now, if we want to multiply this encrypted message with a constant $C$, we can calculate the inner product between the decomposed C and this scaled value. Just like what we have learnt in primary school. I.e., we can decompose $C$ to $\text{Decomp}(C) = (C_{\ell - 1}, \ldots, C_{0})$such that $$ C = \sum_{i = 0}^{\ell -1} C_i 10^i $$ Then the multiplication becomes: $$ C \cdot m = \mathsf{Decomp}(C) \cdot \mathsf{Scale}(m) $$

Toy Example

$m = 6, C = 3405, k = 4$

$$ \begin{align*} \text{Decomp}(C) &= (3, 4, 0, 5)\\ \text{Enc}(m) &= (6000, 600, 60, 6) \\ C \cdot m &= 3 \cdot 6000 + 4 \cdot 600 + 5 \cdot 6 = 20430 \end{align*} $$

Generalization

Instead of 10, we can use larger base ($B = 256$ for example). Then the gadget looks like $\vec{g} = (B^{\ell - 1}, \ldots, B^{0})$.

Denote $g^{-1}(v) := \mathsf{Decomp}_g(v)$. There is a very good property of gadget decomposition: $$ | g^{-1}(v) \cdot g - v|_\infty \leq \epsilon $$

Another level of generalization looks like:

$$ \begin{align*} G= I_k \otimes \vec{g} = \left(\begin{array}{c|c|c} B^{\ell - 1}& \ldots & 0 \\ \vdots & \ddots & \vdots \\ B^0 & \ldots & 0 \\ \hline \vdots & \ddots & \vdots \\ \hline 0 & \ldots & B^{\ell - 1} \\ \vdots & \ddots & \vdots \\ 0 & \ldots & B^0 \end{array}\right) \end{align*} $$
It turns out that this big $G$ here is also a gadget by definition 3.1 in Building an Efficient Lattice Gadget Toolkit: Subgaussian Sampling and More if we treat each row as an element.

Ring-GSW

This is another FHE scheme. The special thing about this scheme is that it uses RLWE and a special gadget matrix during the encryption stage.

$$ \begin{align*} \text{RGSW}(m) = Z + m \cdot G && Z = (\underbrace{\text{RLWE}(0), \ldots, \text{RLWE}(0)}_{2 \ell}), G = I_2 \otimes \vec{g} \end{align*} $$
This is a Ring-GSW sample that encrypts the message $m$ (without scaling by any factor). This is a special case of RGSW (otherwise $G = I_k \otimes \vec{g}$ for any desired $k$. Check TFHE). And, we also have $2\ell$ rows of RLWE(0). This encryption is straight forward. However, I don’t know any decryption methods. Why? Note that some gadget values are very small compared to the ciphertext coefficient modulus, which means $m \cdot g_i$ can be as small as the noise…

External Product

Additive noise growth for ct-ct multiplication!!!

External product using only one gadget decomposition:

$$ \begin{align*} \text{RGSW} \boxdot \text{RLWE} &\to \text{RLWE} \\ (A, b) &\mapsto A \boxdot b = G^{-1}(b) \cdot A \end{align*} $$
English: we first decompose the RLWE ciphertext, and then multiply it with RGSW.

In the context of external product, $\text{Decomp}_G(v) \in R^{1\times2l}, A \in R^{2l \times 2}$.

Proof sketch

Let $\text{msg}(A) = \mu_A, \text{msg}(b) = \mu_b$. By definition of RLWE, $b = (a, a \cdot s + \mu_b + e) = (a, a \cdot s + 0 + e) + (0, \mu_b) = z_b + (0, \mu_b)$.

$$ \begin{align*} A \boxdot b &= G^{-1}(b) \cdot A = G^{-1}(b) \cdot (Z_A + \mu_A \cdot G)\\ &= G^{-1}(b) \cdot Z_A + \mu_A \cdot (G^{-1}(b) \cdot G)\\ &= G^{-1}(b) \cdot Z_A + \mu_A \cdot (\epsilon + b)\\ &= G^{-1}(b) \cdot Z_A + \mu_A \cdot \epsilon + \mu_A \cdot (z_b + (0, \mu_b))\\ &= G^{-1}(b) \cdot Z_A + \mu_A \cdot \epsilon + \mu_A \cdot z_b + (0, \mu_A \cdot \mu_b)\\ \end{align*} $$

Decryption is to calculate the linear equation $\varphi_s(;(a, b);) = b - a \cdot s$. Then, rounding the result, everything goes to zero except $\mu_A \cdot \mu_b$.

Why this is good?

Check the noise growth! The advantage for doing this is the first term $G^{-1}(b) \cdot A$. If we don’t do the gadget decomposition, say $G^{-1}(b) = b$, and $A$ is a vector, then this term multiplies the error of two messages together. However, because of the gadget decomposition, the error term inside $b$ is upper bounded by $B$. The total error looks like:

$$ \begin{align*} \| \text{Err}(A \boxdot b) \|_\infty\leq \| G^{-1}(b) \cdot \text{Err}(A) \|_\infty + |\mu_A| \cdot \epsilon + |\mu_A| \cdot \text{Err}(b)\\ \text{Roughly: } O(B \cdot \text{Err}(A) + |\mu_A| \cdot \text{Err}(b)) \end{align*} $$

If we have small message $\mu_A$, then this multiplication is roughly free! I must quote this sentence I learnt from Jeremy Kun: “This is useful when the noise growth is asymmetric in the two arguments, and so basically you make the noise-heavy part as small as possible and move the powers of 2 to the other side.”

The essence is that we separate RLWE, which is very sensitive to scaling, to smaller parts, and then perform this “digit-by-digit” multiplication. We can do this because we have carefully designed this RGSW scheme so that it stores enough information for all powers of $B$, saving this scaling for RLWE.

Key Switching

In RLWE, key switching is a technique that helps us change the underlying secret key without decrypting the ciphertext. Formally, we want to change the underlying secret key from $s$ to $t$:

$$ \begin{align*} c = (a, b) \;\;\; &\longrightarrow \;\;\; c' = (a', b')\\ c = (a, a \cdot s + m + e) \;\;\; &\longrightarrow \;\;\; c' = (a', a' \cdot t + m + e')\\ \end{align*} $$
Definition Key Switching Key(KSK) $$ \mathsf{KSK}(s, t) = \mathsf{RLWE}t(s) = (x, x \cdot t + s + e{\text{new}}) $$ where $x \in \mathbb{Z}_q[X] / (x^n + 1)$ is another random polynomial. This is a new ciphertext encrypting the old secret key.

Then, the new ciphertext $c’$ can be computed by:

$$ \begin{align*} c' &= (0, b) - a \mathsf{KSK} \\ &= (0, b) - (a x, a (x t + s + e_{\text{new}}))\\ &= -(ax, (a x t + a s + a e_{\text{new}}) - b)\\ &= -(ax, (a x t + a s + a e_{\text{new}}) - (as + m + e))\\ &= (-ax, -a x t + m + (e - ae_{\text{new}}))\\ &= (a', a't + m + e') \end{align*} $$
Observe that this is still a valid RLWE ciphertext. Here is another way to to check if $c’$ has correctly encrypted the message $m$ under the key $t$. We check this by applying the phase function (or simply decrypt it):
$$ \begin{align*} \varphi_t(c') &= \varphi_t(\; (0, b) - a \cdot \mathsf{KSK}\;)\\ &= \varphi_t((0, b)) - a \cdot \varphi_t(\mathsf{KSK})\\ &= (b - 0 \cdot t) - a \cdot (s + e_{\text{new}})\\ &= (b - a \cdot s) - a \cdot e_{\text{new}}\\ &= m + e - a \cdot e_{\text{new}}\\ \end{align*} $$
This is consistant with the aboved result.

HOWEVER, the error $a \cdot e_\text{new}$ can be too large! $a$ is randomly sampled in $\mathbb{Z}_q[X] / (x^n + 1)$. The trick is to use Gadget Decomposition! Decomposing $a$ into smaller chunks, and scaling the underlying message inside KSK into different levels, without scaling up the error.

$$ \begin{align*} &\text{Scaling this up: }\mathsf{KSK}(s, t)'_i = \mathsf{RLWE}_t^*(sB^i) = (x, x \cdot t + sB_i + e_{\text{new}}), i = 0, \ldots, \ell - 1\\ &\text{Decomposing this: }a \Rightarrow G^{-1}(a) = \set{a_i : i = 0, \ldots l-1} \end{align*} $$
The new ciphertext is computed:
$$ \begin{align*} c' &= (0, b) - G^{-1}(a) \cdot \mathsf{KSK}(s, t)'\\ &= (0, b) - \sum_{i = 0}^{\ell-1}G^{-1}(a)_i \cdot \mathsf{KSK}(s, t)'_i \end{align*} $$
Check the phase of this ciphertext:
$$ \begin{align*} \varphi_t(c') &= \varphi(0, b) - \sum_{i = 0}^{\ell-1}G^{-1}(a)_i \cdot \varphi_t \left( \mathsf{KSK}(s, t)'_i \right)\\ &= b - \sum_{i = 0}^{\ell - 1} G^{-1}(a) \cdot (sB_i + e_i)\\ &= b - s \cdot (G^{-1}(a) \cdot G) - \sum_{i = 0}^{\ell - 1}\underbrace{G^{-1}(a)}_{\mathcal{O}(B)} \cdot e_i\\ &= b - a \cdot s + e' \end{align*} $$

Substitution / Frobenius Automorphism

The underlying $X$ is multiplied by $k$. So the term $X^i \mapsto X^{ik}$: $$ \mathsf{Subs}(\mathsf{RLWE}(\mu(X)), k) = \mathsf{RLWE}(\mu(X^k)) $$ This can be implemented using the key switching algorithm.

Essence: to apply the Frobenius automorphism on the message, we have to apply it to the whole ciphertext. But we can use a new key $s(X^k)$ to replace $s(X)$ to cancel the changes in the random part $a(X) \mapsto a(X^k)$. Then, decrypting the message leaves only the message $\mu(X^k)$. We don’t care the error term because the variance of the error is not changed.

References: